Heap sort is a comparison-based sorting algorithm that uses a binary heap data structure. Heap sort has two main steps: building a max heap from the input list and repeatedly extracting the max element from the heap, and appending it to the sorted list.

Heap sort saves time by maintaining the unsorted region in a heap data structure to quickly find the largest element in each step, where in selection sort, heap sort does not perform linear-time scans of the unsorted region.

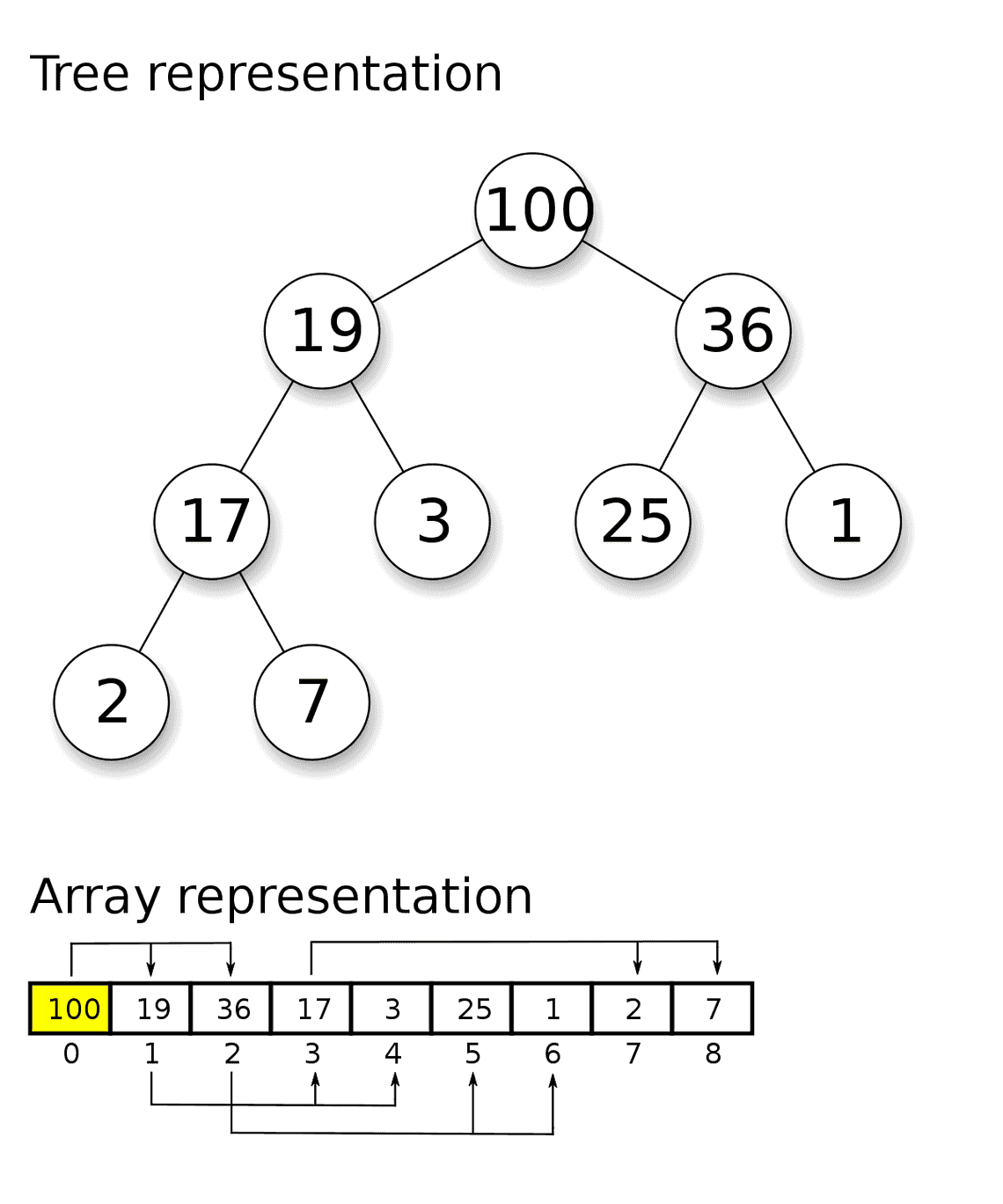
Implementation

Heap sort starts by building a max heap from the input list, then repeatedly swapping the first element of the heap with the last element and decrementing the size of the heap. Heapify is called after each swap.

def heap_sort(arr):
    n = len(arr)

    # Max heap
    for i in range(n, -1, -1):
        heapify(arr, n, i)

    # One by one extract elements
    for i in range(n - 1, 0, -1):
        # swap
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, i, 0)
    return arr

Heapify

Our heapify function is used to maintain the max-heap property of the heap.

def heapify(arr, n, i):
    # Largest = root
    largest = i
    # Left
    l = 2 * i + 1
    # Right
    r = 2 * i + 2

    # Check if left child of root exists and is greater than root
    if l < n and arr[i] < arr[l]:
        largest = l

    # Check if right child of root exists and is greater than root
    if r < n and arr[largest] < arr[r]:
        largest = r

    # If needed, change root
    if largest != i:
        # Swap
        arr[i], arr[largest] = arr[largest], arr[i]
        # Heapify root
        heapify(arr, n, largest)

Sorted array is: 
[11, 22, 33, 44, 77, 99]

Heap sort has a time complexity of O(n log n). This ranks this algorithm more efficient than selection and bubble sorting algorithms. Heap sort is an in-place sorting algorithm and doesn’t require additional memory.

Heapq module

We can make our implementation more efficient by using the built-in python heapq module which uses the heap queue algorithm. We convert our array to a max heap by passing each element to the heapify function. Then repeatedly extracting the first element which is the maximum element of the heap and append it to the sorted list.

import heapq

def heap_sort(arr):
    # Convert array to max heap
    heap = [x for x in arr]
    heapq.heapify(heap)

    # Pull element from heap
    sorted_arr = [heapq.heappop(heap) for _ in range(len(arr))]
    return sorted_arr

arr = [44,11,77,22,99,33]

print("Sorted array is: ")
print(heap_sort(arr))

Sorted array is: 
[11, 22, 33, 44, 77, 99]

For descending order:

heap = [-x for x in arr]
    heapq.heapify(heap)
    
    # Pull element from heap
    sorted_arr = [-heapq.heappop(heap) for _ in range(len(arr))]
    return sorted_arr

Sorted array is: 
[99, 77, 44, 33, 22, 11]